On the largest length scales in the universe, the distances between galaxies become awkward to define. The universe is continuously expanding, and the light of these objects takes many millions of years to reach us. This means that these objects may be vastly further away today than they were when their light set out on its journey across the universe to reach us.

To make sense of this, cosmologists have devised a variety of ways of defining the distances to objects.

Redshift

The light of objects which are receding from us is shifted to longer wavelengths – towards the red end of the visible spectrum – due to the Doppler Effect. This affects all objects at cosmological distances, which are invariably receding from the Earth due to the continuous expansion of the Universe.

With a spectrograph, this wavelength shift is quite easy to measure very precisely, since it produces a shift in the wavelengths of sharply-defined spectral lines, as compared to their positions in laboratory measurements. Redshift is defined as:

where \( \lambda_\mathrm{o} \) is the observed wavelength of a spectral feature in the spectrum of a distant object, and \( \lambda_\mathrm{e} \) is the laboratory wavelength of that feature.

As a measure of distance, redshift has the advantage that it is directly measurable. It forms the observational evidence from which astronomers infer the distances of most distant galaxies, by using some cosmological model to convert from redshift to distance.

Look-back time

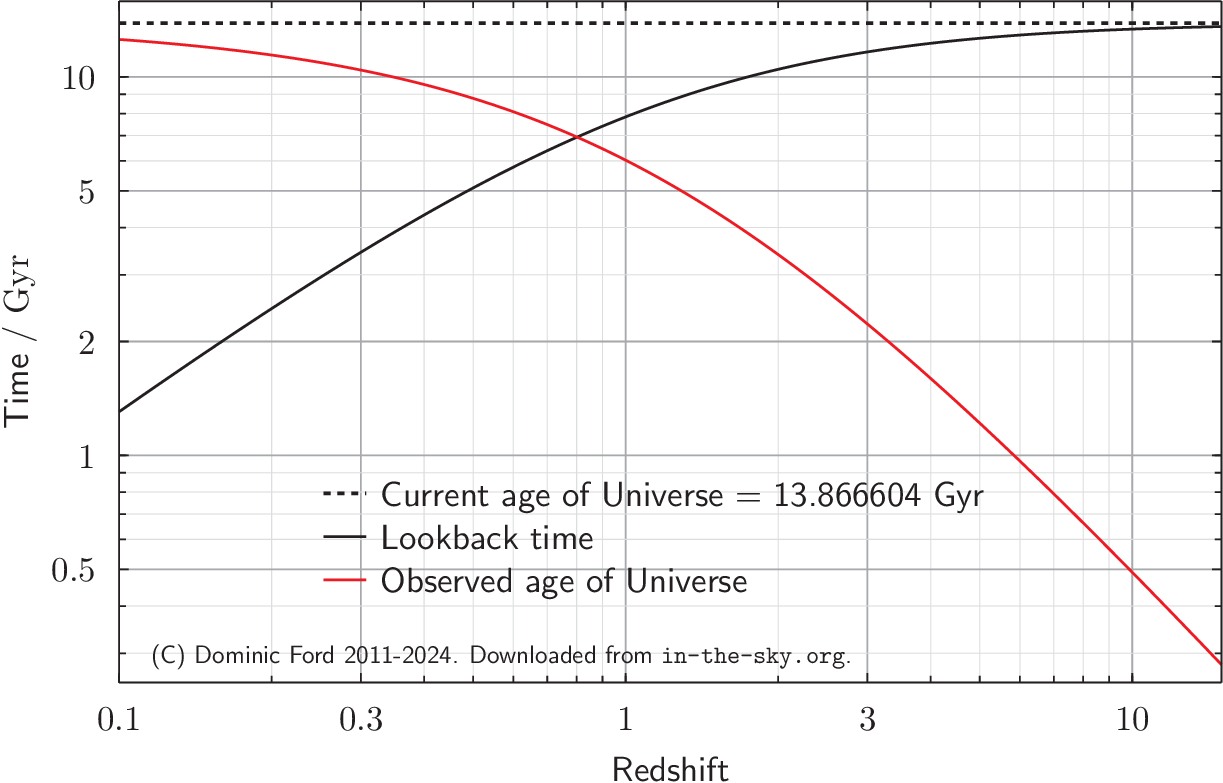
The look-back time to an object is the time taken for its light to reach us. This tells us how far back into cosmic history we are looking when we observe a particular galaxy. It also tells us how far the light has travelled to reach us, as the universe expanded around it. This distance can be found simply by multiplying the object's look-back time by the speed of light.

The plot below shows the look-back time of objects as a function of their redshifts \( z \). The red line shows age of the Universe at the moment when the object's light that we see today set out towards us. Observations of objects at redshift \( z \) show us a picture how the universe appeared at the age indicated by the red line. This figure is also available in pdf and png formats.

Proper motion distance

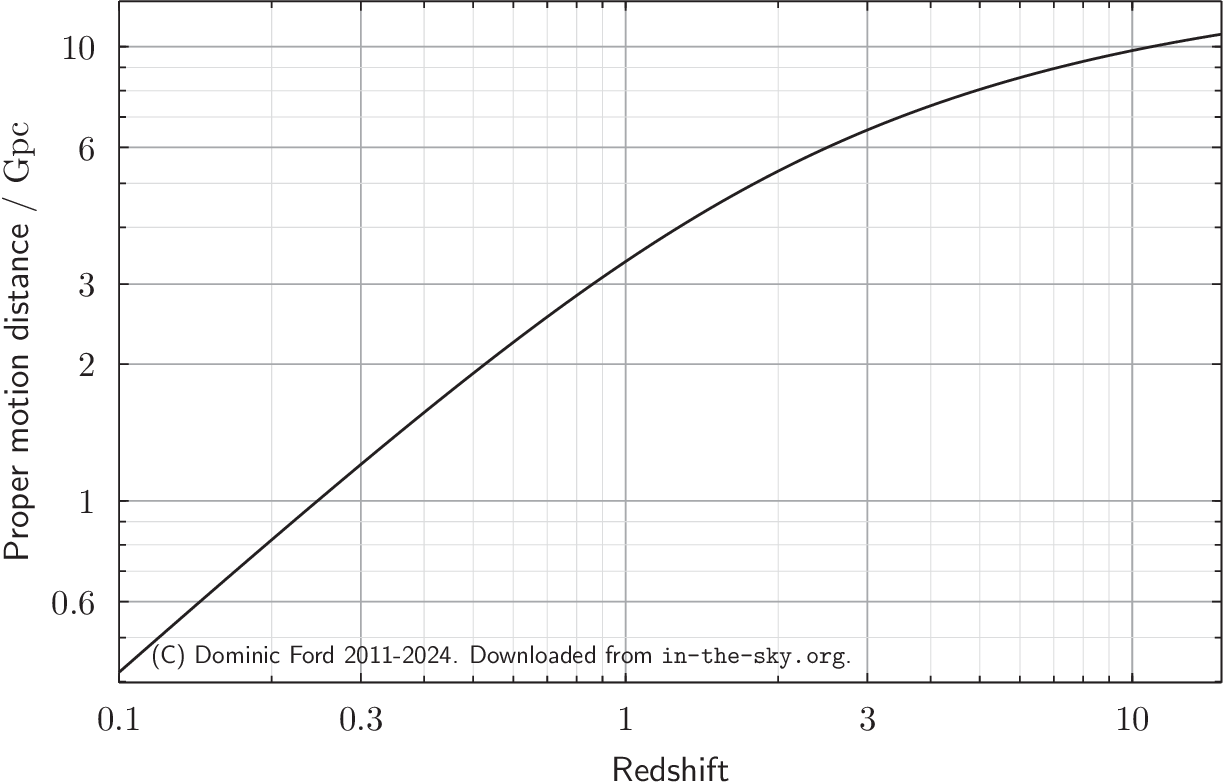
The proper motion distance to an object is perhaps the most simple and intuitive definition of distance, though it's also one of the least useful.

Imagine freezing the whole universe at some particular time, and measuring the distance between two objects with a tape measure at that particular instant. This is the proper motion distance.

The reason why this is not particularly useful is that such tape measures don't really exist, and the distances to far-away galaxies are typically vastly greater today than they were when the light that we see from them set out.

The plot below shows how the proper motion distances of galaxies increases with redshift \( z \). This figure is also available in pdf and png formats.

Luminosity distance

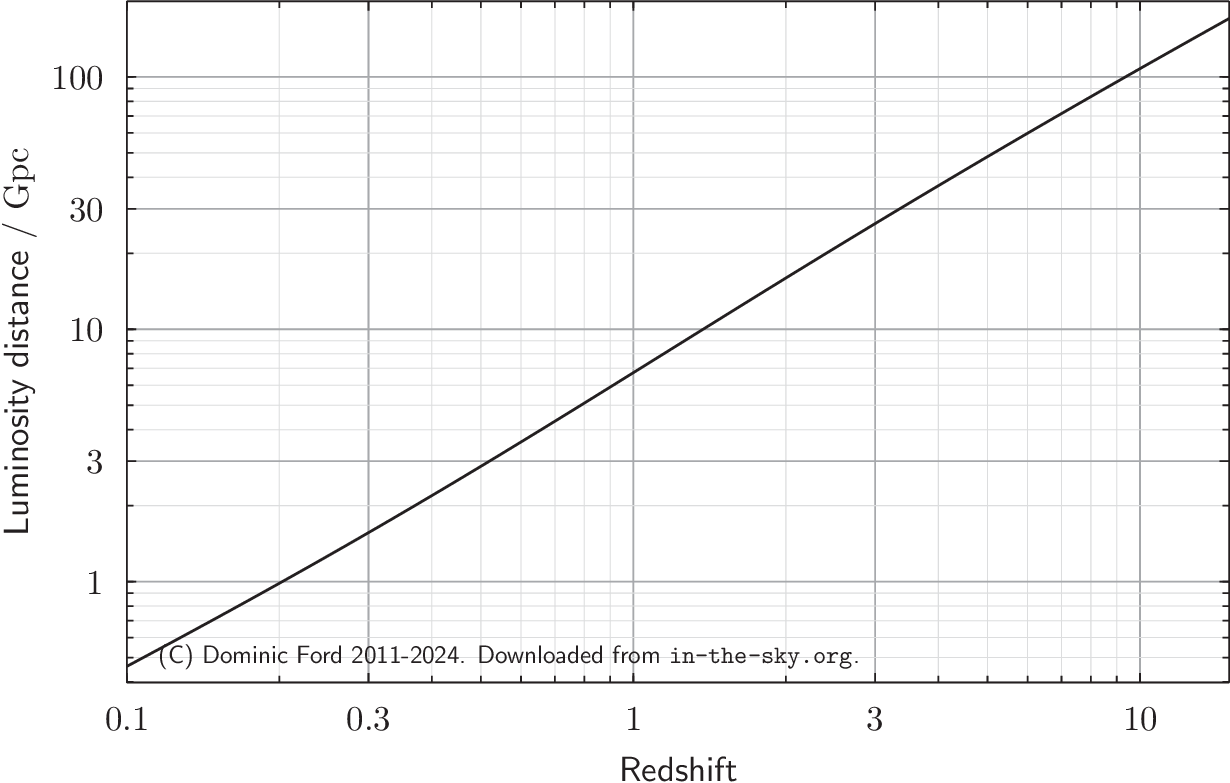
In the nearby universe, objects become fainter the further they are away. An object's brightness decreases with the square of its distance, according to the formula:

where flux is a measure of the rate at which light arrives, and \( D_\text{L} \) is the distance of the object. This relation is useful, because it allows the distances of objects to be measured from their observed brightnesses, if their intrinsic luminosities can be estimated.

The luminosity distance \( D_\text{L} \) of an object is simply an extension of the formula above to apply to more distant objects. \( D_\text{L} \) is defined such that the equation above holds, given the luminosity of an object, and its observed brightness when observed from afar.

The plot below shows how luminosity distance \( D_\text{L} \) varies with redshift. This figure is also available in pdf and png formats.

Angular size distance

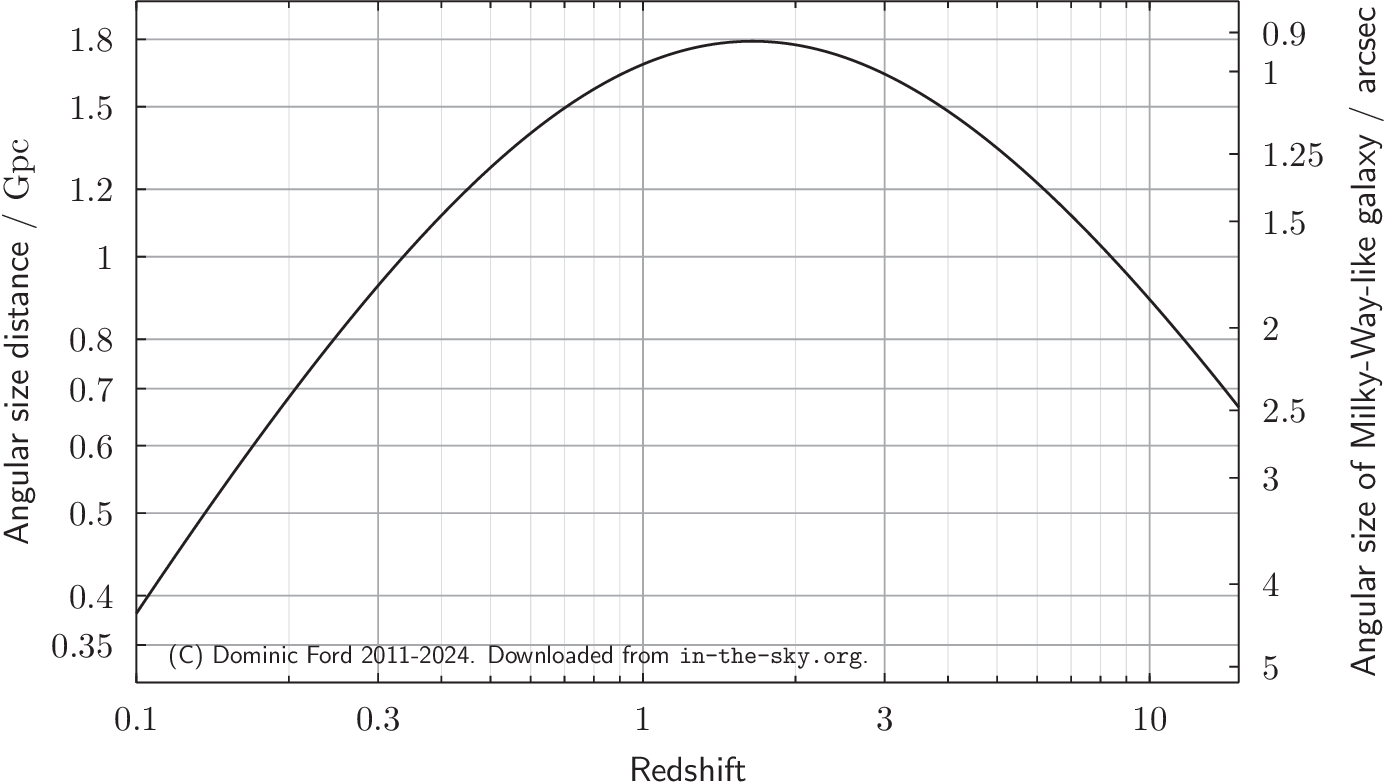
In the nearby universe, objects also get smaller the further they are away. An object's apparent angular size decreases with distance according to the formula:

where \( \frac{D}{D_\text{A}} \) is the distance of the object and \( a \) is the physical diameter of the object. In this expression, I have assumed that \( \text{arctan}(x) \approx x \), which is true for objects that cover less than several square degrees of sky.

As above, the angular size distance \( D_\text{A} \) of an object is simply an extension of this formula. Thus, \( D_\text{A} \) is defined such that the equation above holds.

The plot below show how the angular size distance of objects change with redshift. This definition of distance is perhaps the most strange and counter-intuitive, in that it reaches a maximum at a redshift of around \( z=1.8 \), and decreases for more distant objects.

In the very distant past, the universe was much smaller than it is today. As a result, galaxies back then would have filled a significantly larger fraction of the universe than an identically-sized galaxy would do today. It is this that makes the very most distant galaxies cover larger areas of the sky than nearer galaxies of the same size.

The figure below is also available in pdf and png formats.

More information

The plots on this page necessarily assume some particular cosmological model for the expansion of the Universe. I have used a standard Λ-CDM cosmology, with the cosmological parameters \( H_0=70 \), \( \Omega_\text{m}=0.27 \) and \( \Omega_\Lambda=0.73 \). In recent years, observations by the WMAP and Planck spacecraft have placed very tight constraints on these cosmological parameters, and so it is possible to make precise statements about the distances to very remote objects that would not have been possible before 2003.

On this page, all distances are expressed in Gpc, where 1 Gpc equals 3.26 billion lightyears.

For more information and mathematical details about cosmological distances, see David Hogg's article Distance measures in cosmology . Note that Hogg's article pre-dates the modern era of precision cosmology, heralded by the WMAP spacecraft, and so his statements about the uncertainty in cosmological models are now surprisingly dated. Hogg, D., Distance measures in cosmology, astro-ph 9905116v4

Share