A leap second is a one-second adjustment which is applied to our system of timekeeping every few years, to keep the time of day shown by clocks synchronised with the movement of the Sun across the sky.

They are necessary because the Sun's position in the sky is governed by the rate at which the Earth turns on its polar axis, and this varies very slightly over time. Processes such as earthquakes, ocean currents, and energy losses due to the changing tides, can all make minute changes to the Earth's rotation speed.

By contrast, atomic clocks, and other highly accurate physical processes, proceed at a constant rate which is set by physics unrelated to the Earth's rotation.

In modern times, we have chosen to define time using atomic clocks, rather than measurements of the Sun's position. This is essential for modern science, so that highly precise laboratory measurements of how long processes do not produce different results depending on how fast the Earth is rotating at the time.

This introduces the possibility, however, that our definition of the time of day might slip out of synchronisation with the daylight hours.

Leap seconds are the correction factor which is introduced to ensure they stay aligned.

A brief history of timekeeping

In medieval times, the time of day was judged by the position of the Sun in the sky. When the Sun was highest in the sky, it was midday. The time interval until midday the next day was divided into 24 hours.

For many reasons, this system was unsatisfactory. Aside from the fact that it's impossible to observe the Sun's position in bad weather, the exact moment when the Sun is at its highest in any given town depends on that town's east-west longitude. It may differ by five minutes in two towns 100 miles apart.

The advent of long distance train lines and radio communications in the nineteenth century led to a standardisation of time between towns. Whole countries, or timezones within countries, chose to adopt common national time standards. For example, the whole of Britain uses Greenwich Mean Time in the winter, which is based on when noon occurs in London.

Mechanical clocks

In medieval times, time might often have been measured with a sundial, but in more recent centuries, we have grown to prefer mechanical or electronic machines as a means to measure time.

This development has ancient roots: hourglasses and water clocks were used in ancient Egypt. The increasing reliability of clockwork mechanisms in the 15th and 16th centuries meant that mechanical clocks became more widespread, even if a typical town might only have one clock.

As clocks gradually became more durable, affordable, and accurate, they became increasingly ubiquitous. But still, they did not keep perfect time and they needed to be corrected from time to time. This was inevitably done with reference to some measurement of the Sun's position in the sky.

This changed, however, once it became clear that the Earth's rotation speed was changing.

Detection of changes in the Earth's rotation

In the 18th and early 19th century, astronomers questioned whether the Earth's rotation rate was constant and could be relied upon as a fixed indicator of the passage of time. They failed, however, to observe any evidence that the Earth's rotation was changing speed.

We now know that the fluctuations in the length of each day are at the level of a few milliseconds. This was simply too small to be measured until the early twentieth century. By the 1920s, however, evidence of fluctuations was mounting.

Astronomers were able to make precise measurements of the timings of various unrelated astronomical phenomena, and identify anomalies in their measurements which were correlated between the various phenomena. This implied that the anomalies were not caused by the individual phenomena, but were instead intrinsic to the common system of timekeeping used to make all the measurements.

For the first time, it seemed that the precision of scientific timing experiments was not limited by the apparatus used, but by the definition of time itself.

Ephemeris time

This realisation led to the first attempts to create a system of ephemeris time, which would be defined by astronomical phenomena such as the orbits of the planets. These were believed to follow a much more regular pulse than the Earth's rotation.

The first such standard was created in 1952, and used the Earth's motion around the Sun to keep track of time. This was assumed – rightly – to be stable over much longer time periods than the Earth's own rotation.

In the new system, the length of each hour was arbitrarily chosen to be one twenty-fourth of the length of January 1, 1900, and the new hours were counted from midnight on that day. This system was named ephemeris time (ET), and was used primarily by astronomers who needed the best possible time standard to keep track of the orbits of the objects in the solar system over long periods.

Atomic time

Within a very few years, technology provided a more workable solution. In 1955, the first accurate atomic clock was built by the National Physical Laboratory (NPL) in the UK, making use of the discovery that atoms produce light waves of very well defined frequencies (i.e. colors) when electrically excited.

The 1955 clock worked by counting the cycles of microwave emission produced by caesium-133 atoms, which radiate at a very well-defined frequency of around 9.2 GHz when kept in well controlled conditions.

Modern atomic clocks – which still often use caesium-133 atoms – can now keep time with an accuracy better than one second in 100 million years. Whereas in the past, timekeeping relied on astronomical observatories to make high precision measurements of the Sun's position, it is now possible for anybody with a few tens of thousands of US dollars to purchase their own very accurate time standard.

Since 1972, ephemeris time has been superseded by international atomic time (TAI), defined such that each second is exactly the time taken for a caesium-133 atom to produce 9,192,631,770 cycles of microwave radiation. This definition was chosen so that TAI clocks read the same time, and used the same length of second, at the moment of the transition from ET.

Synchronising the Sun with atomic time

While the fixed pulse of atomic time is a great convenience for scientists, detaching the definition of time from the Earth's daily rotation introduces the risk that over time, the hours of daylight might drift out of alignment with the time read by clocks following TAI.

The Earth's rotation rate is now known to be gradually slowing down, primarily because rotational energy is lost through the rising and falling tides each time the Earth turns on its axis. By contrast, each 24-hour period in TAI is fixed to the length of the first day of the 20th century.

It is inevitable, then, that such misalignment will grow over time. In a few thousand years' time, it is expected that the Sun's passage across the sky will take one second longer than it does today. By then, solar time will drift by a rate of over six minutes (360 seconds) per year relative to the fixed 24-hour periods measured by the current definition of international atomic time.

To avoid this problem, since 1972 civil time has been defined using a system called coordinated universal time (UTC), which is distinct from atomic time. The two systems run at the same rate, but whenever UTC is found to disagree with the observed position of the Sun in the sky by more than half a second, a second is either inserted into or subtracted from UTC, causing a particular minute to have either 59 or 61 seconds.

At present, the task of monitoring the Earth's rotation is managed by the International Earth Rotation and Reference Systems Service (IERS), which ultimately decides when such leap seconds should be added. To date, the Earth has always been found to have been rotating more slowly than it was in 1900, and so seconds have been added rather than taken away, at a rate of roughly one every two years. By custom, such seconds are added at midnight, Greenwich time, on either January 1st or July 1st.

The offset between atomic time and universal time is recorded by a quantity called ΔT, though for historical reasons ΔT actually equals this time offset plus an additional 32.184 seconds. Strictly speaking, ΔT records the offset between another time standard, terrestrial time, and universal time, where terrestrial time lags atomic time by exactly 32.184 seconds.

Historical values of ΔT

The historical offset between universal time and atomic time provides an insight into the historical rate of the Earth's rotation. Remarkably, historical records exist which allow it to be estimated many centuries in the past.

For example, observers in past centuries often noted the exact times at which they saw lunar occultations and eclipses. Modern computer models of the Moon's orbit allow the timing of its passage through the solar system to be traced with sub-second accuracy – in modern atomic time – even thousands of years in the past.

Eyewitnesses from past centuries tell us the time of day, using local solar time, at which these events took place. With suitable correction, the difference between their solar time measurements and modern atomic time calculations is a measure of the historical value of ΔT.

Prior to the invention of the telescope in 1609, eclipses were the only observable events whose timing was sufficiently sharply defined that they can now provide such points of reference. In recent years, Prof Richard Stephenson at Durham University has pioneered the study of them.

In the telescopic era, occultations of stars by the Moon provide a much more frequent stream of historical events which were often observed and recorded with high precision.

Present-day measurements of ΔT rely on high-precision measurements of sidereal time using radio telescopes. This is done using very distant quasars, which are so distant – typically billions of light-years away – that their positions among the constellations can be assumed to be absolutely fixed. Any tiny irregularity in their daily motion across the sky can be attributed entirely to the Earth's rotation. The high resolution of radio telescopes means that the position of quasars can be directly compared with atomic clocks to determine the Earth's rotation rate.

Reconstructing historical values of ΔT from all this of data reveals a chaotic variability (see below) over the past four hundred years. These wiggles are due to short-term phenomena such as earthquakes and ocean currents, which overwhelm the long-term slowing of the Earth's rotation, even on century-long timescales.

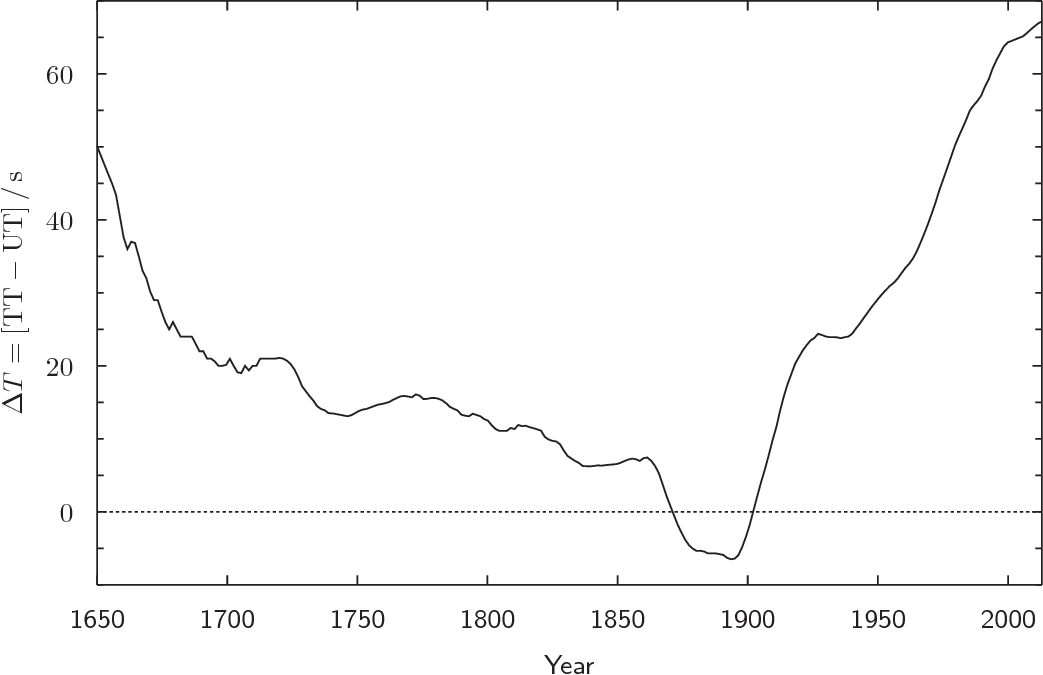
The offset between terrestrial time (TT) and universal time (UT) is called ΔT. Terrestrial time, for historical reasons, runs in step with international atomic time, but 32.184 seconds ahead.

Looking back further using historical eclipse observations, Richard Stephenson has been able to estimate the historical length of days over the past 3,000 years.

A particularly clear-cut demonstration that days have grown longer is a set of observations of the total solar eclipse of April 15, 136 BC, which was observed from Babylon. Modern computations of the Moon's orbit, combined with a naive assumption that the Earth has been rotating at a constant rate over the intervening years, find that the Moon was indeed aligned to produce a total solar eclipse on that day, but that its shadow didn't pass anywhere near Babylon. Instead, it passed along the west coast of Africa, some 50° in longitude (3 hours) to Babylon's west.

The Earth's rate of rotation has no effect on the alignment of the Sun and Moon that produced the eclipse, but it did affect which landmass lay beneath the Moon's shadow at this particular moment in 136 BC. The Earth's faster rate of rotation in past centuries has added up to produce a full 50° of additional rotation over the intervening 2,200 years.

Based on data such as this, the graph below shows Stephenson's best estimate of the historical lengths of days over the past three-thousand years, expressed as an offset in milliseconds from their present length of 86,400 modern seconds. Extending the data back further still, it is likely that days lasted only 22 modern hours at the time of the dinosaurs, 65 million years ago.

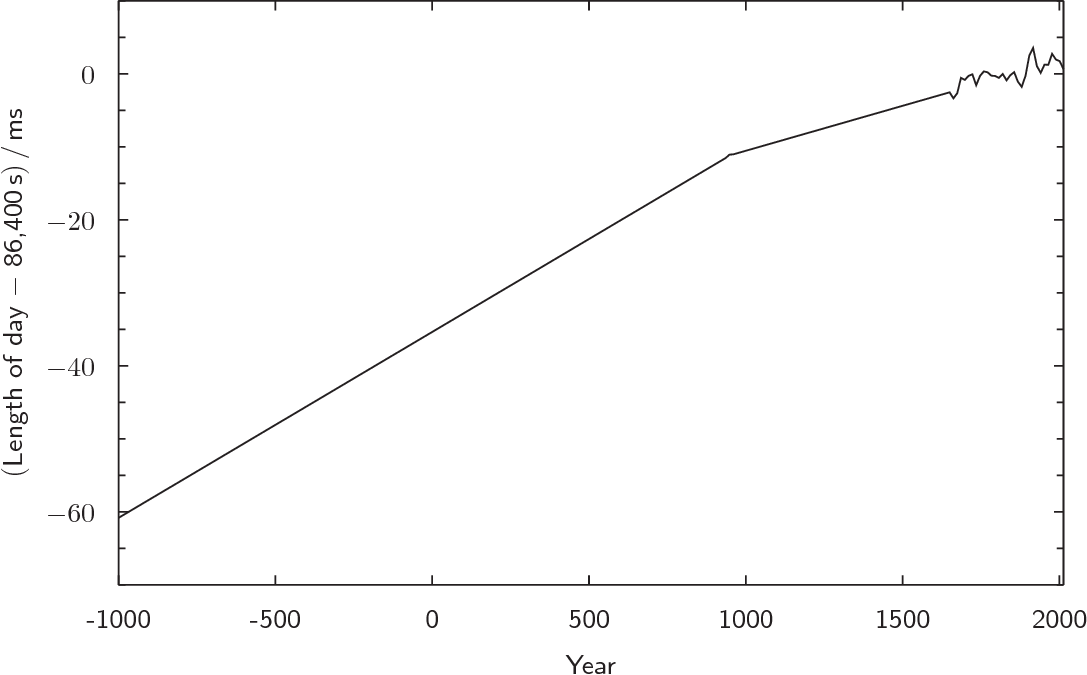
Estimates of the historical length of day, based primarily on historical observations of lunar occultations and eclipses. Before the twentieth century it was impossible to detect short-term variations in the Earth's rotation, and so the reconstructed curve appears much smoother. In the period since it has been possible to detect short-term variability, it has dwarfed the long-term gradual lengthening of days.

The future of leap seconds

In recent years, there has been growing debate about the future of leap seconds. Some argue that they should be abolished because they make our calendar excessively complicated. For example, two observations of Mars, made at exactly 11pm on June 30, 2012 and 1am on July 1, 2012 in UTC, are actually separated by two hours and one second. This is only apparent, however, to somebody who happens to have an up-to-date list of leap seconds to hand.

Furthermore, it is completely impossible to do such arithmetic with future dates – to ask when a 30-second process will finish, if started at 23:59:50 on December 31, 2100 – as leap seconds are usually only announced six months in advance. This is an especial problem for computer software: on June 30, 2012, there were reported cases of computer systems crashing when their clocks appeared to stand still for a second.

In the near term, the benefit from having leap seconds is small, since few people would notice if noon were to systematically drift by a few seconds later in the day. Over coming centuries, if the Earth's rotation continues to slows down at the average rate that it has done over past centuries, leap seconds will have to be added at an ever-increasing rate. By 2250, leap seconds may be needed every year, and by 3000, three may be needed each year. Arguably, it may make more sense by then to redefine the length of each day to be a little longer, rather than to make such frequent adjustments to our clocks.

Share