Equation Of Time
The Earth, as seen by the Apollo 17 astronauts. Image courtesy of NASA.
The equation of time is a measure of the slight variation in the length of each day depending on the time of year.
In some months, days can be up to 20 seconds longer or shorter than 24 hours, in a predictable pattern which repeats every year. This arises from two effects:
- The rate of the Sun's eastward movement through the constellations changes over the course of the year. It is fastest at the solstices, and slowest at the equinoxes.
- The Earth's orbit around the Sun is not a perfect circle, but is slightly elliptical. This means that its orbital speed changes through the year.
Both these effects very slightly alter the rate of movement of the Sun across the sky, adding or subtracting a few seconds from the time it takes to get from noon on one day to noon the next day.
Clocks, however, continue to run at a constant rate at all times of year. This means that, at those times of year when days are shorter than 24 hours, noon drifts earlier in the day. When days are longer than 24 hours, the noon comes later each day.
The time shown by clocks is called mean time, because it is based on the average (or mean) length of the day through the year. The time system we call Greenwich mean time (GMT) is based on the mean time at the Greenwich Observatory in London. By defining the length of each day in this way, we ensure that although the time of noon varies through the year, it comes back to (almost) the same time on the same day of each year.
The equation of time is defined as the offset between mean time and solar time. Solar time is judged by the position of the Sun in the sky, where midday is the moment when the Sun appears highest in the sky on every day of the year. Over the course of the year, solar time can deviate from mean time by more than 15 minutes from mean time.
This offset explains why, for example, sundials often include conversions between the solar time that they measure, and the mean time system that clocks read.
Sidereal time
In crude terms, our daily cycle of day and night results from the Earth's rotation about its polar axis once every 24 hours. As it rotates, the Sun moves across the sky. Once in each revolution, the Sun is highest in the sky, at noon. Twelve hours later, the Sun is lowest in the sky – usually some distance below the horizon.
The simple picture glosses over a few details. Firstly, the Earth doesn't rotate once every 24 hours, but a little faster than that. It turns once every 23 hours and 56 minutes.
This is the time it takes stars in the night sky to revolve around the celestial poles, called the sidereal day. Any particular star will rise at exactly the same point on an observer's horizon every 23 hours and 56 minutes.
We define the time of day, however, not by the positions of stars in the sky, but by the position of the Sun.
Unlike the stars, the Sun moves a significant distance through the constellations from one day to the next – by around a degree, or twice its diameter. This eastward motion is in the opposite direction to the sky's apparent westerly daily rotation. After each sidereal day, the stars return to the same positions, but the Sun is a full two Sun-widths behind where it appeared the previous day. It takes the sky's rotation just under four minutes to turn this extra distance.
As a result, stars traverse the sky once every 23 hours and 56 minutes, but the Sun does so once every 24 hours.
Seasonal changes
In practice, there is an additional complication. This four-minute difference between the sidereal day and the solar day is not the same every day.
The chart below shows the Sun's annual path through the constellations of the zodiac – along the ecliptic – projected onto a rectangular grid of right ascension and declination.
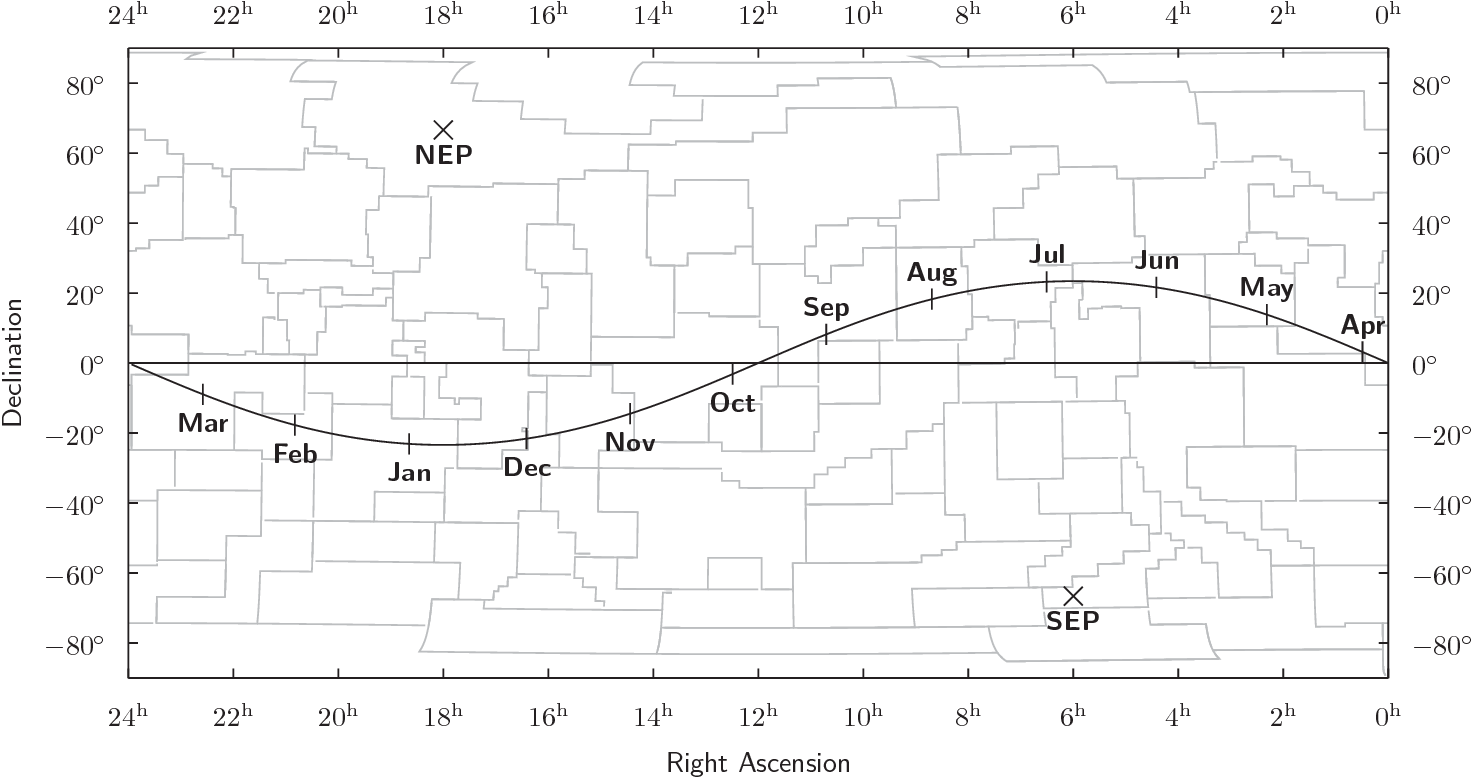
The Sun moves leftward (eastward) across the map by an average of one degree, or four minutes in right ascension, each day. But its path is not a straight line.
At the solstices, the Sun's north-south movement in declination comes to a standstill at the tropics. The Sun is moving horizontally (eastwards) across the map above, with no north-south motion.
As the Sun passes the celestial equator at the equinoxes, it moves along a diagonal path with considerable north-south as well as eastward motion. At these times, the Sun's rate of motion in declination is at its greatest.
There is a corresponding variation in the Sun's rate of eastward movement in right ascension. At the equinoxes, when it traces a diagonal line, it moves comparatively slowly in right ascension. Conversely, at the solstices, when the Sun moves along a horizontal line, its right ascension changes comparatively quickly.
This has the effect that the four additional minutes, in addition to the length of a sidereal day, that separate noon one day from noon the next, is slightly more than four minutes at the solstices, and slightly less at the equinoxes.
The Earth's elliptical orbit
There is a second contibution to this variation. The Earth's orbit is not quite circular, but oval shaped – an ellipse. It makes its closest approach to the Sun around January 3, and is furthest from the Sun around July 4.
According to Kepler's laws of planetary motion, planets move more quickly when they are closer to the Sun, and more slowly when they are further from the Sun. The Earth is no exception, and the Sun's apparent rate of motion along the ecliptic changes with the Earth's distance from the Sun. It moves fastest in January, and slowest in July.
The combined effect
The combination of the two effects above causes the length of each day to vary by up to 20 seconds through the year. In June and December, it takes the Sun less time to get from noon one day to noon the next, as compared to March and September.
As a result, in local solar time the length of the second changes slightly depending on the time of year. Seconds pass more quickly in June and December than in March or September. With the advent of accurate mechanical clocks, it has become preferably to find a definition of the length of the second that is constant throughout the year.
Mean time
Mean time is just such a system. The length of each second is constant throughout the year, defined to be one 86,400th of the average time it takes the Sun to move from noon on one day to noon on the following day.
On any given day of the year, the length of the solar day may differ by up to 20 seconds from this, and since these errors accumulate day by day, the time at which noon occurs according to a clock showing mean time may drift at a rate of up to ten minutes per month relative to solar time.
However, the length of the mean day is chosen such that there is an exact balance between the times of year when noon drifts earlier in the day, and those when it drifts later in the day. After one whole year has elapsed, noon has returned to exactly the same mean time.
The equation of time
In a mean time system, the time interval between noon – when the Sun is highest – and midday – when clocks read 12:00 – is called the equation of time. The word equation is used in a historical sense, not to mean an algebraic expression but rather a correction.
Although the equation of time varies by up to 20 minutes through the course of the year, it repeats almost exactly the same pattern each year, since the Earth follows almost exactly the same path around the Sun from one year to the next.
The figure below shows difference, in minutes, between solar time and mean time over the course of the year (click to enlarge it). It is also available in pdf and png formats.
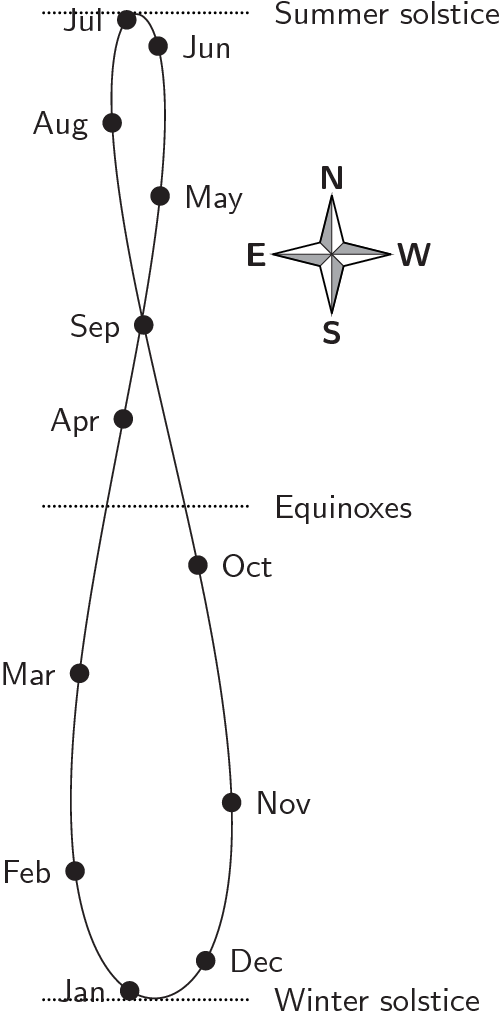
The Sun's analemma
Suppose that a photograph is taken at exactly midday in mean time each day, recording the Sun's position in the sky.
As the seasons change, the Sun's altitude at midday changes: it culminates at a higher altitude in the summer than in the winter.
However, the Sun's east-west position also varies through the year because of the equation of time. At some times of year, it will appear further to the east, still approaching its highest point in the sky at midday. At other times it will appear further to the west, having already passed its highest point in the sky.
The result is a figure-of-eight pattern called an analemma. The diagram below shows the analemma that would be recorded by a northern-hemisphere observer, with circles indicating the position of the Sun on the first day of each month.
The same pattern would also be seen in the southern hemisphere, viewed upside down and with the summer and winter solstices swapped.