8. The Shadow Scale

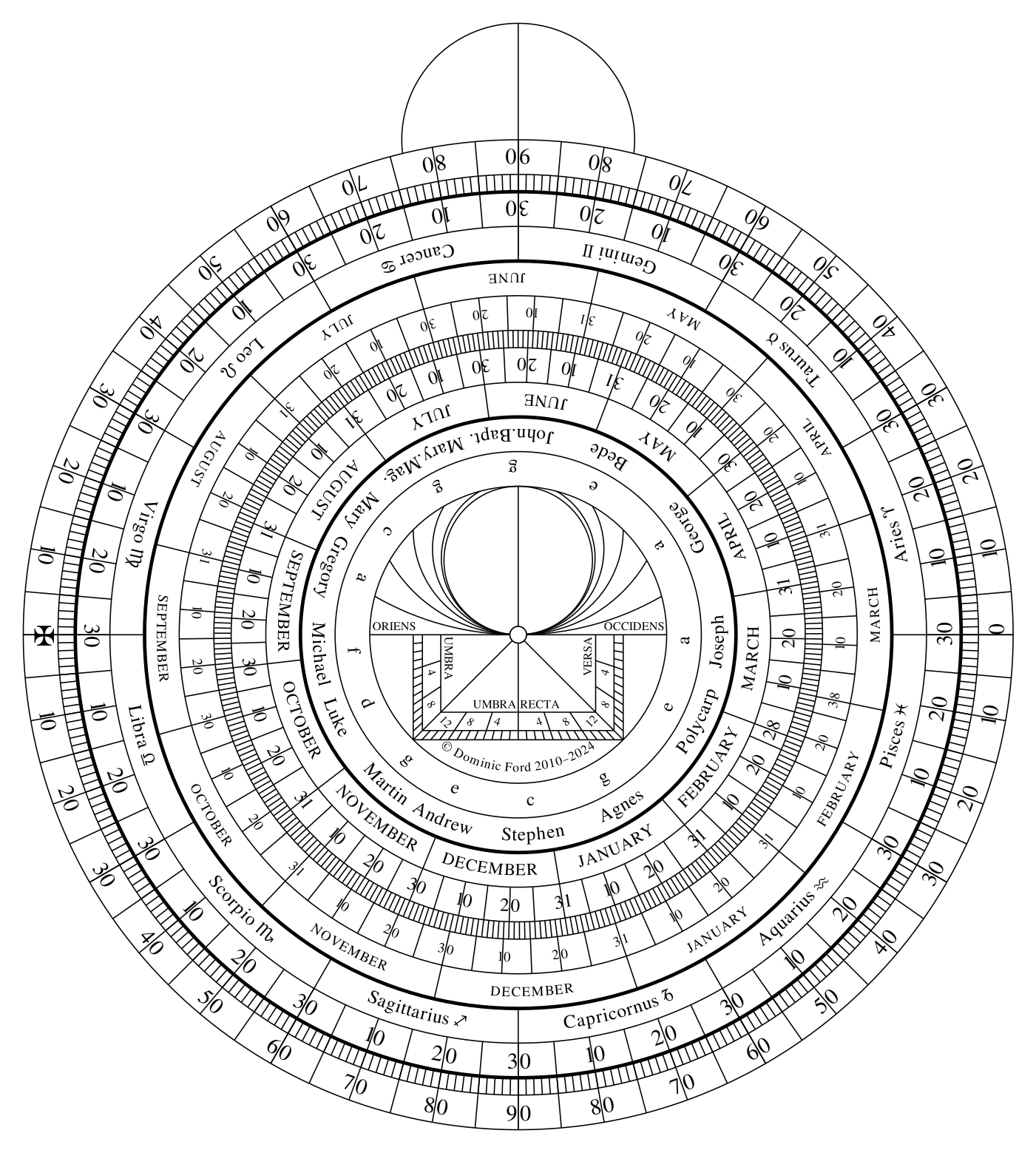
We now turn to one of the few non-astronomical applications of the astrolabe. This is the shadow scale, in the lower half of the central portion of the reverse side of the mother, where Latin words "Umbra" and "Recta" appear.

The problem is this: suppose that you see a tall building, and you want to know how tall it is. The shadow scale provides a means of relating the height of the building to its distance away from you. Providing you have some means of knowing its distance, either by looking at a map, or by pacing out the distance, the astrolabe will tell you the building's height.

Conversely, if you already know how tall the building is, but want to know how far away it is, the shadow scale will allow you to estimate this conversion.

The first step is to measure the elevation of the top of the building above the horizon, in degrees, by sighting it along to alidade as described previously. The shadow scale will then convert this elevation in degrees into the ratio between the building's height and its distance.

The range of elevations between 0° and 45° is divided into twelve parts, with lines denoting the points where the ratio of height to distance is 1/12, 2/12, ..., 12/12. The line where the ratio is 4/12, for example, is labelled '4': this corresponds to buildings that are at a distance of three times their height.

The use of twelve as a denominator here is a good choice – much better than ten, for example – because of its having six factors: thus 3/12 equals 1/4, 4/12 equals 1/3, etc. Thus, when a building's highest point is at the altitude labeled '4', its height is four twelfths – or one third – of its distance.

At an altitude of 45°, the ratio becomes 12/12, or in simpler terms, 1/1. This means that the building's height is equal to its distance. Higher altitudes are similarly labelled with numbers between 1 and 12, denoting the points where the ratio equals 12/11, 12/10, ..., 12/1.

Mathematical note

Presented with the task of determining the distance d of a building of known height h using an observation of the altitude θ of its highest point, we would probably turn to trigonometry nowadays. Children learn in school that in a right-angled triangle, the function tan(θ) is equal to the ratio of the lengths of the side opposite to the angle, and the side adjacent to the angle. Hence, the tangent of a building's elevation θ equals the ratio of its height to its distance, or h/d.

Reaching for a calculator, it is easy to calculate the height of a building as d/tan θ, or the distance of a building as h×tan θ. The astrolabe's shadow scale is essentially an easy look-up table of the function tan θ.