3. The Back of the Mother

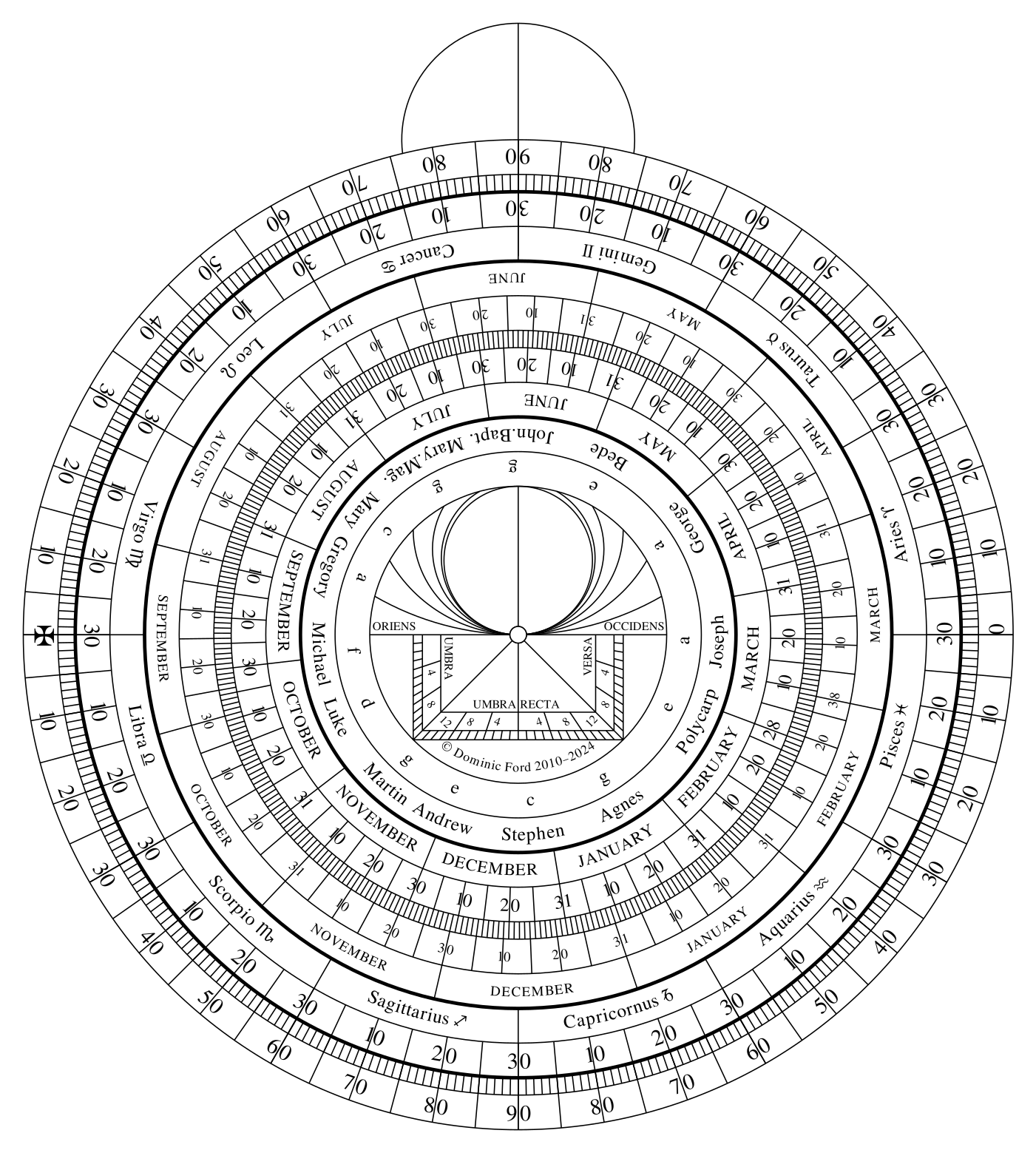
The image to the right shows the back of the mother of the astrolabe. Over the top of this the alidade is allowed to freely rotate, like the hands of a clock, around a central pivot. It acts as a measuring ruler and a simple observing instrument. Two tabs fold out from the edges of the alidade to act as a simple sight.

Most of the circles on the back of the mother form a calendar, referencing the time of year to the Sun's annual motion along through the constellations of the ecliptic. One full revolution around the disc represents one year.

Measuring the elevation of stars

In many of the calculations described in the following pages, it will be necessary to measure the elevation (altitude) of stars above the horizon.

To do so, the astrolabe should first be suspended at eye level, such that you are able to look along the length of the alidade. Traditionally, the astrolabe would be suspended from a ring hooked over the user's right thumb. When using a cardboard astrolabe, I would recommend punching a small hole through the handle protruding from the top of the astrolabe, and attaching a loop of string or ribbon through it. You may then suspend the astrolabe by holding this loop in your hand, or hooking it over a finger.

It is important, however, that the astrolabe should hang freely, so that the zero marks on the back of the mother are horizontal, while the 90° marker points towards the zenith.

While looking along the line of the alidade, you should rotate it until your sight line along it lines up with your sight line to the star you want to measure. Once this is done, the outermost scale on the astrolabe will indicate the star's altitude in degrees.

The Sun's path

The Sun's path through the ecliptic constellations is divided into twelve equal 30° portions, and each portion designated as a zodiacal constellation. The first of these, Aries, is defined to start at the vernal equinox, the point on the sky where the Sun's path crosses the equator in March. It ends when the Sun has moved 30° eastwards from the vernal equinox, which happens after roughly a month.

These ancient zodiacal constellations bear little relation to the 88 modern constellations known to astronomers today. The latter are a much newer creation which were only finalised by the International Astronomical Union (IAU) as a definitive list in 1922 and given rigid boundaries in 1930. The modern constellations have widely varying sizes, and at the moment of the vernal equinox, the Sun lies in Pisces rather than Aries.

On the astrolabe, a circle names the twelve zodiacal constellations, dividing the year into portions when the Sun passes through each of them. Inside of this circle, a more traditional calendar provides a conversion to the familiar system of days and months. Following Sigmund Eisner's example (my design is based heavily on his series of three papers in the Journal of the British Astronomical Association), two calendars are shown.

Calendar dates in 1394 and 1974

The outer calendar, in smaller typeface, is computed for 1394, around the time of Chaucer's composition, using solar longitude data published by Tuckerman (1962, 1964). This calendar should be used if you would like to read Geoffrey Chaucer's original Treatise on the Astrolabe. The inner calendar is computed for 1974 – taken as the present day – and should be used for modern observations and calculations.

These two calendars are offset by nine days relative to each other, which can be explained by the calendrical reforms which took place between 1394 and 1974, which shifted the date of the vernal equinox by a total of nine days.

In 1394, the Julian calendar had been in use in Britain since Roman times, assigning every fourth year as a leap year, and giving each year an average length of 365.25 days. The Earth's seasons in fact repeat once every 365.2422 days (once per tropical year), which is some 11 minutes shorter than the Julian calendar's year.

As a result, the date of the vernal equinox gradually drifted later in the year, by around one day every 128 years. This problem was resolved with the introduction of the Gregorian calendar, which removed three leap years in every 400 years. At the same time, 11 days were removed from the British calendar in 1752 to restore the equinox to its traditional date of March 21, used for calculating the date of Easter since the time of the Council of Nicaea (325 CE).

The drift of the Gregorian calendar relative to the seasons is so slight – 10–20 seconds per year – that the seasons slip by only one day every few thousand years. Consequently, the calendar presented by Sigmund Eisner for 1974 remains accurate for modern use.

The years 1394 and 1974, are significant, however, in that they fall midway between leap years. In a normal 365-day year, the timing of the vernal equinox drifts by a quarter of a day from one year to the next. It shifts back to its original position in the fourth year, when a leap day is added. These midpoint years consequently represent an average over this slight four-year variation in the precise date and time of the equinoxes.

The Christian liturgical year

Even further towards the centre of the astrolabe, a scale shows the names of a number of significant Christian saints, marking their feast days, together with their Sunday letters. In past times these would have been a selection of locally revered saints; I have simply selected a few of the best known. This circle reminds us that the astrolabe was not purely a tool for science: an ancient astrolabe was as likely to have been found in the hands of a priest as an astronomer.

The innermost markings, lying within the circle of saints, are called the shadow scale and will be described in a later section.