| Start: | Wed, 04 Feb 2065 at 23:40 PST (07:40 UTC) |
| End: | Thu, 05 Feb 2065 at 04:02 PST (12:02 UTC) |
14,294 days away
Dominic Ford, Editor
From
the Eclipses
feed
The Moon will pass in front of the Sun, creating a partial eclipse of the Sun visible from Africa, western Russia, Europe and Asia between 23:40 and 04:02 PST.
From the Contiguous United States, no eclipse will be visible (change location ).
In the northern hemisphere, a maximum of 86% of the Sun's disk will be eclipsed by the Moon, but nowhere on Earth will see a total solar eclipse. This is because nowhere on Earth will see a perfect alignment between the Sun and Moon in the sky.
Mapping provided by https://hilltopviews.org.uk
The outermost red contour on the map above traces where in the world the eclipse will be visible – i.e., where the Moon will cover any part of the Sun's disk. Within this, the thinner red contours show where the Moon will cover at least 20%, 40%, 60% and 80% of the Sun at the moment of greatest eclipse.
This map is also available as a KMZ overlay which can be imported into Google Earth, Google Maps, or other mapping software, to create a more detailed map. Alternatively, it can be downloaded as a non-interactive image in PNG, PDF or SVG format.
The animation above shows the progress of the Moon's shadow across the Earth as the eclipse proceeds. The red circle shows the edge of the Moon's shadow: all places inside the red circle will see the Moon covering some part of the Sun's disk. Within this, the yellow contours show where various fractions of the Sun's disk is covered.
The eclipse path
The path of the eclipse will pass through countries including:
| Country | Percentage of Sun eclipsed |
Start time (UTC) |
End time (UTC) |
| France | 78% | 08:17 | 11:23 |
| Ireland | 83% | 08:25 | 11:10 |
| Great Britain | 84% | 08:25 | 11:20 |
| Jersey | 78% | 08:27 | 11:10 |
| Guernsey | 78% | 08:27 | 11:10 |
| Northern Ireland | 83% | 08:32 | 11:12 |
| Isle of Man | 82% | 08:35 | 11:13 |
| Orkney | 83% | 08:45 | 11:20 |
| Faroe Islands | 84% | 08:47 | 11:18 |
| Shetland | 82% | 08:48 | 11:23 |
| Norway | 79% | 08:52 | 11:48 |
| Iceland | 86% | 09:37 | 11:17 |
The eclipse geometry

Solar eclipses occur when the Sun, Moon and Earth are aligned in a straight line, so that the Moon passes between us and the Sun and blocks its light.
Each time the Moon orbits the Earth, it comes close to the Sun in the sky as it passes New Moon. If the Moon orbited the Earth in exactly the same plane that the Earth orbits the Sun, it would pass in front of the Sun at New Moon every month.
But in fact the Moon's orbit is tipped up at an angle of 5° relative to the Earth's orbit around the Sun. This means that the alignment between the Moon and Sun at New Moon usually isn't exact. Normally, the Moon passes a few degrees to the side of the Sun.
In the diagram to the right, the grid represents the plane of the Earth's orbit around the Sun. As it circles the Earth, the Moon passes through this Earth–Sun plane twice each month, at the points on the left and right labelled as nodes. A solar eclipse happens only when one of these node crossings happens to coincide with New Moon. This happens roughly once every six months.
Even when solar eclipses do occur, they are not visible from the whole world.
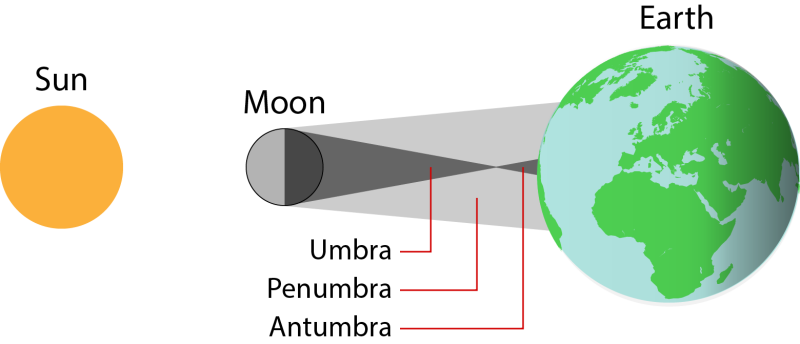
The Moon is much smaller than the Earth, and the shadow it casts onto the Earth is never more than a few hundred miles across. The diagram to the right is not drawn to scale, but gives an approximate sense of how much of the Earth's surface can be covered by the Moon's shadow at any one time. As the Moon travels along its orbit, its shadow sweeps across the Earth, usually travelling from west to east at a speed which varies between 1,000 and 5,000 mph.
The Moon's shadow can be divided into the umbra, indicated as a dark gray cone, where the Moon appears to completely cover the Sun, and the larger penumbra, where the Moon only partially covers the Sun.
The umbra gets narrower at greater distances from the Moon, since the Moon covers less of the sky when seen from greater distances, and so needs to be more precisely aligned in order to cover the entire Sun. At a distance of 373,000 km, the Moon appears with exactly the same angular size as the Sun, and so the umbra narrows to a single point where the two objects are perfectly aligned in the sky.
As seen from the Earth, the Moon is only just large enough to cover the Sun. The Sun's angular diameter varies over the course of the year between 0.542 degrees (January) to 0.524 degrees (July) due to the Earth's elliptical orbit. The Moon's angular diameter likewise varies between 0.548 degrees and 0.490 degrees.
When the Earth and Moon are at their closest, the umbral shadow projects a circle onto the Earth's surface with a diameter of 170 miles, within which a total solar eclipse can be seen. But when the Earth is at its furthest from the Moon, the planet falls beyond the furthest limit of the Moon's umbral shadow and the Moon appears too small to entirely cover the Sun's disk. This gives rise to the possibility of annular eclipses, where a complete ring of sunlight is formed around the Moon.
The region of space where annular eclipses are seen lies beyond the furthest tip of the umbra at a distance of 373,000 km from the Moon, in a third region of shadow called the antumbra.
The diagram above was not drawn to scale, so as to make the three regions of the Moon's shadow large enough to see. In practice, all celestial bodies are much smaller than the distances which separate them, and the Earth and Moon are no exception. The diagram below shows the Earth and Moon drawn to scale, together with the Moon's shadow spanning the space between them. As above, the light gray region shows the Moon's penumbra, and the dark gray region shows the Moon's umbra.
The Earth is drawn twice, at its closest and furthest possible distances from the Moon – distances of around 363,000 km and 405,000 km respectively. The cross marks the maximum extent of the Moon's umbra – the furthest distance from Moon at which a total eclipse is possible (373,000 km).

Eclipse safety
Observing the Sun can be very dangerous if it is not done with the right equipment. The Sun is the brightest object in the sky, and looking directly at it can cause permanent eye damage within seconds. Viewing it through any optical instrument – even a pair of binoculars or the finderscope on the side of a telescope – can cause instant and permanent blindness.
If you have any doubts about whether your equipment is safe, it is best not to risk using it. By far the safest thing to do is to go along to a public observing event. Many astronomical societies are likely to be hosting observing events on the day, and they'll be sure to welcome newcomers. You may meet some new people at the same time as seeing the eclipse.
Many astronomy suppliers sell special special filters which can be fitted to telescopes to make them safe for solar viewing. These include aluminised mylar filters, or black polymer filters, identified as suitable for direct viewing of the Sun. Check that the filter has a CE mark, and a statement that it conforms to European Community Directive 89/686/EEC. Alternatively, you can use a welder's glass rated at No. 14 or higher. Always read the manufacturer's instructions carefully.
Never attempt to make your own filter. In addition to visible light, the Sun also produces prodigious amounts of infrared and ultraviolet radiation which cannot be seen yet can still damage your eye. Even if a homebrew filter appears adequate, it may allow this unseen radiation to pass.
Projecting an image of the Sun
Another safe way to view solar eclipses is to buy a purpose-built solar projection box.
These typically consist of a cardboard box with a small lens on one side. They project an enlarged image of the Sun onto a white cardboard sheet inside the box. Once the eclipse is over, they're also great for observing sunspots. They are safe to use, quick to set up, and ideal for use with children and groups.
Further details
This eclipse is a member of Saros series 151. The position of the Sun at the moment of greatest eclipse will be:
| Object | Right Ascension | Declination | Constellation | Angular Size |
| Sun (center) | 21h14m | 15°57'S | Capricornus | 32'26" |
The coordinates above are given in J2000.0.
Next/previous eclipses
| « Previous | Next » | |||
| Visible from the Contiguous United States | Worldwide | Worldwide | Visible from the Contiguous United States | |
| 27 Jan 2055 | 03 Sep 2062 | Partial Solar Eclipses | 03 Jul 2065 | 24 Nov 2068 |
| 16 Jan 2056 | 12 Aug 2064 | Solar Eclipses | 03 Jul 2065 | 24 Nov 2068 |
| 22 Jan 2065 | 22 Jan 2065 | Eclipses | 03 Jul 2065 | 11 Jan 2066 |
The sky on 17 Dec 2025
| The sky on 17 December 2025 | ||||||||||||||||||||||||||||||||||
|
3% 27 days old |
All times shown in PST.
|
|||||||||||||||||||||||||||||||||
Warning
Never attempt to point a pair of binoculars or a telescope at an object close to the Sun. Doing so may result in immediate and permanent blindness.
Source
|
[1] – |
The eclipse maps presented on this website were computed using EclipseSimulator. This is an open-source tool which traces the positions of the Sun, Earth and Moon over the course of each eclipse and traces the path of the Moon's shadow across the Earth's surface. It was written by the author and freely available for download from GitHub. EclipseSimulator takes the positions of each body from the JPL DE430 planetary ephemeris. It treats the Earth and Moon as ellipsoids with the same polar and equatorial radii which are also assumed by Fred Espenak's eclipse predictions. All eclipse predictions are made at sea level. The predictions here match those calculated by Xavier Jubier to within a few kilometers. |
|
[2] – |
Espanak, F., & Meeus, J., Five Millennium Canon of Solar Eclipses: -1999 to +3000, NASA Technical Publication TP-2006-214141 (2006) |
|
[3] – |
The list of countries from which the eclipse is visible was computed on the basis of shape files available from DIVA-GIS. |
License
You may embed the animations and images above in your own website. They are licensed under the Creative Commons Attribution 3.0 Unported license, which allows you to copy and/or modify them, so long as you credit In-The-Sky.org.
You can download them from:
https://in-the-sky.org/news/eclipses/solar_20650205_B.mp4
https://in-the-sky.org/news/eclipses/solar_20650205_A.mp4
https://in-the-sky.org/news/eclipses/solar_20650205.png
https://in-the-sky.org/news/eclipses/solar_20650205.pdf
https://in-the-sky.org/news/eclipses/solar_20650205.svg
Image credit
© Jerry Kickhart, Los Osos, California.


